| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 알고리즘
- 취미
- react
- IT자격증
- 프로그래머스
- 프로그래밍
- 코드잇
- 테스팅 자격증
- 미켈란젤로
- 소묘
- clean code
- Python
- Kriss 재택
- 연필
- 클린 코드
- 코딩테스트
- 토익 환급
- leetcode
- IT 자격증
- 그림
- PrivateRouter
- 코딩
- 웹개발
- 색연필
- 다비드상
- KSTQB
- 재택근무
- 파이썬
- csts
- 연필소묘
- Today
- Total
글모음
[프로그래머스] Python 알고리즘 스터디 - 3주차 Searching 본문
3주 차
Searching
< 1. 세 소수의 합 >
1) backtracking 사용
def find_primes(n):
a = [False,False] + [True] * (n -1)
primes=[]
for i in range(2, n + 1):
if a[i]:
primes.append(i)
for j in range(2 * i, n + 1, i):
a[j] = False
return primes
def solution(n):
primes = find_primes(n)
cnt = 0
def count_sum(total_sum, level, res, num_cnt):
nonlocal cnt
if total_sum > n: return
if level == len(primes): return
if num_cnt == 3:
if total_sum == n:
cnt += 1
else:
count_sum(total_sum + primes[level] ,level + 1, res + [primes[level]], num_cnt + 1)
count_sum(total_sum, level + 1, res, num_cnt)
count_sum(0, 0, [], 0)
return cntfind_prime 함수로 소수를 리스트를 만들고 backtracking을 해준다.
backtracking을 사용해서 풀면 정확성은 전부 통과하는데 일부 테스트에서 실패했다..
효율성 단 2개 때문에 다시 짜야하는 슬픔..
세 소수의 합보다 사탕 담기 문제를 더 먼저 풀었는데, 사탕 담기는 backtracking으로 전부 다 통과가 되기에 이 문제도 괜찮을 줄 알았다..


2) combination 적용
from itertools import combinations
def get_primes(n):
is_prime = [False, False] + [True] * (n - 2)
for i in range(int(n // 2) + 1):
if is_prime[i]:
for j in range(i * i, n, i):
is_prime[j] = False
return [i for i, p in enumerate(is_prime) if p]
def solution(n):
primes = get_primes(n)
return [sum(c) for c in combinations(primes, 3)].count(n)
built-in 모듈은 성능이 좋으니 사용할 수 있으면 최대한 사용하자
< 2. 사탕 담기 >
1) backtracking 사용
def solution(m, weights):
cnt = 0
def fill_candy(cur_weight, level, candy_list):
nonlocal cnt
if cur_weight > m: return
if level == len(weights):
if cur_weight == m:
cnt += 1
else:
fill_candy(cur_weight + weights[level], level +1, candy_list + [weights[level]])
fill_candy(cur_weight, level + 1, candy_list)
fill_candy(0, 0, [])
return cnt
2) Combination 적용
def solution(m, weights):
start = time.time()
answer = []
for i in range(1, len(weights) + 1):
answer += combinations(weights, i)
answer = [1 for x in answer if sum(x) == m]
answer = sum(answer)
return answer
3) 코드 리뷰 + 시간 비교

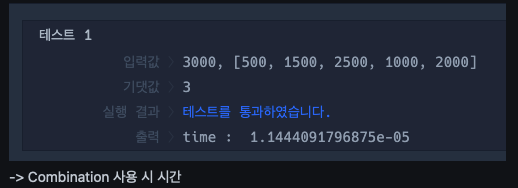
backtracking을 한 코드와 combination을 사용한 코드를 time 모듈로 직접 비교해본 결과,
combination 모듈을 사용한 게 훨씬 빨랐다.
코드 리뷰에서 질문하니 combination 같은 built-in 함수들은 최적화되어 있고, c 코드로 작성되어 있는 경우가 많아 성능이 더 좋은 경우가 많다고 한다.
무조건 문제에 달려들기보다는 좀 더 생각을 해보면서 효율성이 좋은 코드를 짜려고 노력해야겠다.
< 3. 카펫 >
카펫 문제는 탐색 문제보다는 규칙성 찾기 문제에 가깝다고 본다.
import itertools
def solution(brown, red):
candidates = []
for i in range(1, int(red ** (1/2)) + 1):
if not(red % i) :
candidates.append([i, red // i])
for candidate in candidates:
A, B = candidate
cal = A * B + 2 * (A + 2) + 2 * B
if cal == (brown + red):
if A < B : return [B + 2, A + 2]
return [A + 2, B + 2]< 4. N-Queen >
N-Queen은 알고리즘 문제를 풀어봤다면 모르는 사람이 없을 정도로 유명한 문제
1) 나의 풀이(backtracking 사용)
def solution(n):
col = set()
posDiag = set()
negDiag = set()
cnt = 0
def backtrack(r):
if r == n:
cnt += 1
return
for c in range(n):
if c in col or (r + c) in posDiag or (r - c) in negDiag:
continue
col.add(c)
posDiag.add(r + c)
negDiag.add(r - c)
backtrack(r + 1)
col.remove(c)
posDiag.remove(r + c)
negDiag.remove(r - c)
backtrack(0)
return cnt
2) DFS를 사용한 풀이
def check(queen, row):
for i in range(row):
if queen[i] == queen[row] or abs(queen[i] - queen[row]) == row - i:
return False
return True
def search(queen, row):
n = len(queen)
count = 0
if n == row:
return 1
for col in range(n):
queen[row] = col
if check(queen, row):
count += search(queen, row + 1)
return count
def solution(n):
return search([0] * n, 0)< 6. 하노이의 탑 >
하노이의 탑도 N-queen 만큼 유명한 문제다.
def solution(n):
res = []
def hanoi(n, from_pos, to_pos, aux_pos):
nonlocal res
if n == 1:
res.append([from_pos, to_pos])
return
hanoi(n - 1, from_pos, aux_pos, to_pos)
res.append([from_pos, to_pos])
hanoi(n - 1, aux_pos, to_pos, from_pos)
hanoi(n, 1, 3, 2)
return res
후기
3주 차 Searching(완전 탐색)에서는 효율성에서 고생을 많이 했다.
특히 DFS로 구현한 문제들에서 코드는 맞는데 runtime error가 나서 효율성에서 넘어가지 않았다..
DFS는 효율이 정말 좋지 않다는 걸 꼭 기억하자..
이번 주차는 정답을 맞히는 것도 중요하지만 효율성이 좋은 코드를 짜는 것도 중요하다는 걸 느꼈다.
무조건 문제에 달려드는 습관을 버려야겠다.
'알고리즘 > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] Python 알고리즘 스터디 - 4주차 Sorting & Dynamic Programming (0) | 2022.05.30 |
|---|---|
| [프로그래머스] Python 알고리즘 스터디 - 2주차 Stack & Hash (0) | 2022.05.30 |
| [프로그래머스] Python 알고리즘 스터디 - 1주차 Queue & Heap (0) | 2022.05.30 |
| [프로그래머스] 코딩 테스트 알고리즘 스터디(Python) 참여 후기 (9기) (0) | 2022.05.29 |
| [프로그래머스] 폰켓몬 [ Python, level1 ] (0) | 2021.07.21 |



